3 To The 6th Power: Calculation And Example

Raising a number to a power is a fundamental concept in mathematics, and understanding how to calculate it is crucial for various mathematical operations. In this article, we will explore the concept of 3 to the 6th power, how to calculate it, and provide examples to help you grasp the idea better.

What is 3 to the 6th Power?

In mathematics, the expression "3 to the 6th power" is written as 3^6. This means that 3 is multiplied by itself six times. The exponent, in this case, 6, indicates how many times the base number, 3, is multiplied.

Calculation of 3^6

To calculate 3 to the 6th power, you can simply multiply 3 by itself six times:

3^6 = 3 × 3 × 3 × 3 × 3 × 3 = 729

Alternatively, you can use a calculator or a computer program to calculate the result quickly.

Practical Examples

Here are a few examples to help illustrate the concept of 3 to the 6th power:

Example 1: Calculating 3^6 using a calculator

If you enter 3^6 into a calculator, it will display the result as 729.

Example 2: Real-world application of exponentiation

Suppose you have a rectangular prism with a length, width, and height of 3 units each. To find the volume of the prism, you need to calculate the product of the three dimensions:

Volume = length × width × height = 3 × 3 × 3 = 3^3 = 27 cubic units

Now, if you have six such prisms stacked together, the total volume would be:

Total Volume = 3^6 = 729 cubic units

How to Calculate Exponents

Calculating exponents can be a straightforward process if you understand the basic rules. Here are some steps to follow:

Step 1: Identify the base and exponent

In the expression 3^6, 3 is the base, and 6 is the exponent.

Step 2: Multiply the base by itself

Multiply the base, 3, by itself six times: 3 × 3 × 3 × 3 × 3 × 3.

Step 3: Calculate the result

Calculate the product of the six multiplications: 3 × 3 × 3 × 3 × 3 × 3 = 729.

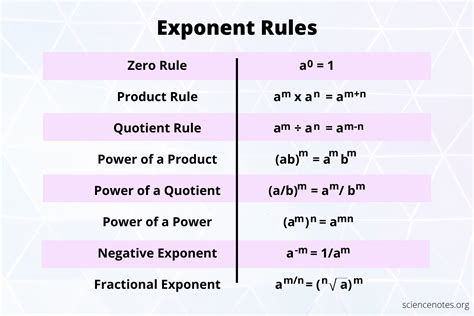
Exponentiation Rules

Here are some essential rules to keep in mind when working with exponents:

Product of powers: When multiplying two numbers with the same base, add the exponents: 3^2 × 3^4 = 3^(2+4) = 3^6.
Power of a power: When raising a power to another power, multiply the exponents: (3^2)^4 = 3^(2×4) = 3^8.
Zero exponent: Any number raised to the power of 0 is equal to 1: 3^0 = 1.

Conclusion

In conclusion, calculating 3 to the 6th power involves multiplying 3 by itself six times, resulting in a value of 729. Understanding exponentiation rules and how to calculate exponents is essential for various mathematical operations. We hope this article has helped you grasp the concept of 3 to the 6th power and how to calculate it.

Now it's your turn! Take a moment to practice calculating exponents and share your thoughts on the importance of understanding this mathematical concept.