Intro
Unlock the secrets of the pentagon shape by exploring its internal angles. Discover how the sum of interior angles in a pentagon adds up to 540 degrees, and learn about the various types of angles, including acute, obtuse, and right angles, that can form inside this five-sided polygon. Dive into the world of geometry and uncover the fascinating math behind pentagons.
The pentagon, a five-sided polygon, is a fascinating shape with a rich history and diverse applications. From architecture to engineering, the pentagon has been employed in various fields due to its unique properties and stability. One of the most intriguing aspects of the pentagon is its angles, which play a crucial role in determining its characteristics and uses.
In this article, we will delve into the world of angles inside a pentagon shape, exploring their types, properties, and applications. Whether you are an architect, engineer, or simply a curious individual, this article aims to provide you with a comprehensive understanding of the angles that make up this incredible shape.
Understanding Angles in a Pentagon
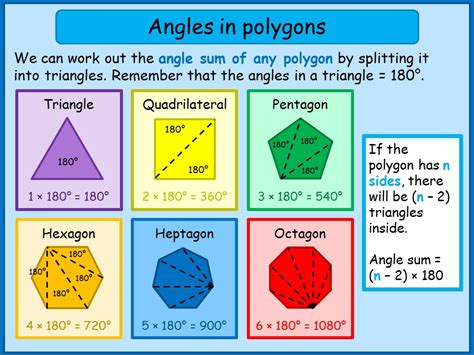
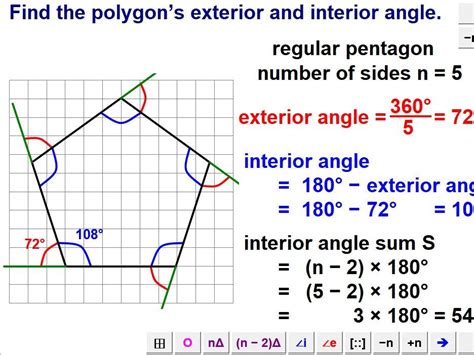
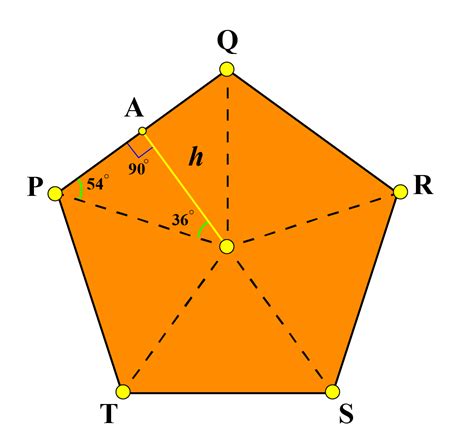
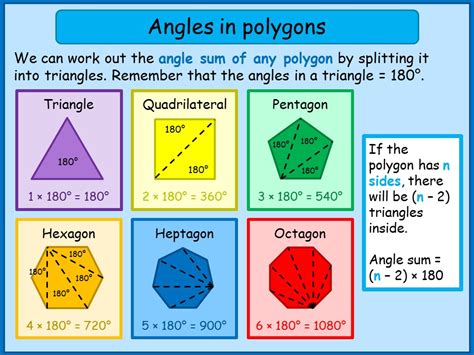
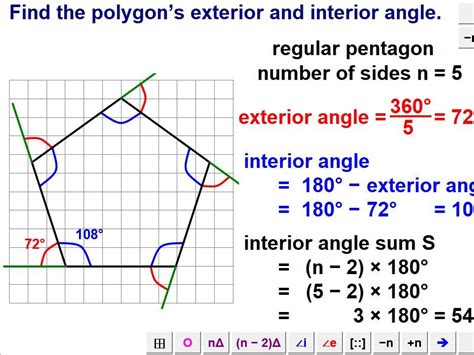
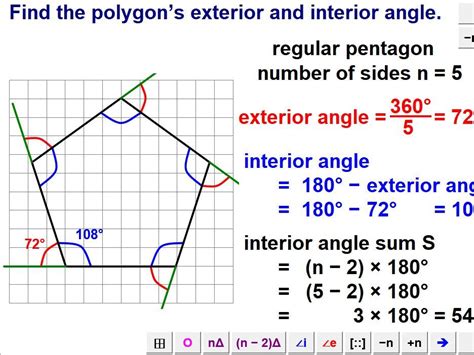
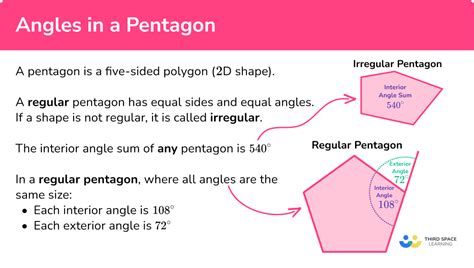
A pentagon is a polygon with five sides, and each internal angle is formed by the intersection of two adjacent sides. The sum of the interior angles of a pentagon is always 540 degrees. This can be calculated using the formula (n-2) × 180, where n is the number of sides. For a pentagon, this becomes (5-2) × 180 = 540 degrees.
Types of Angles in a Pentagon
There are two types of angles in a pentagon: interior angles and exterior angles. Interior angles are the angles formed by the intersection of two adjacent sides, while exterior angles are the angles formed by the extension of two adjacent sides.
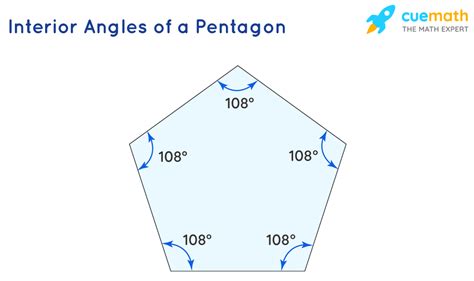
- Interior Angles: The interior angles of a pentagon are the angles formed by the intersection of two adjacent sides. The sum of the interior angles of a pentagon is always 540 degrees.
- Exterior Angles: The exterior angles of a pentagon are the angles formed by the extension of two adjacent sides. The sum of the exterior angles of a pentagon is always 360 degrees.
Properties of Angles in a Pentagon
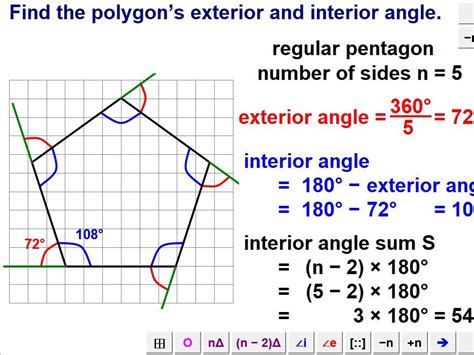
The angles in a pentagon have several interesting properties that make it a unique and fascinating shape.
- Sum of Interior Angles: The sum of the interior angles of a pentagon is always 540 degrees.
- Sum of Exterior Angles: The sum of the exterior angles of a pentagon is always 360 degrees.
- Interior Angle Theorem: The interior angle theorem states that the sum of the interior angles of a polygon is always (n-2) × 180, where n is the number of sides.
- Exterior Angle Theorem: The exterior angle theorem states that the sum of the exterior angles of a polygon is always 360 degrees.
Applications of Angles in a Pentagon
The angles in a pentagon have numerous applications in various fields, including architecture, engineering, and art.
- Architecture: The pentagon is used in architecture due to its stability and unique properties. The angles in a pentagon are used to create visually appealing and functional designs.
- Engineering: The pentagon is used in engineering due to its strength and durability. The angles in a pentagon are used to create stable and efficient structures.
- Art: The pentagon is used in art due to its unique shape and properties. The angles in a pentagon are used to create visually appealing and thought-provoking designs.
Calculating Angles in a Pentagon
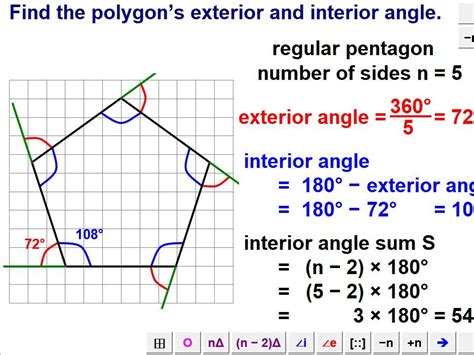
Calculating the angles in a pentagon can be done using various formulas and theorems.
- Interior Angle Formula: The interior angle formula is used to calculate the sum of the interior angles of a polygon. The formula is (n-2) × 180, where n is the number of sides.
- Exterior Angle Formula: The exterior angle formula is used to calculate the sum of the exterior angles of a polygon. The formula is 360 degrees.
- Angle Sum Theorem: The angle sum theorem is used to calculate the sum of the interior angles of a polygon. The theorem states that the sum of the interior angles of a polygon is always (n-2) × 180, where n is the number of sides.
Practical Examples of Angles in a Pentagon
The angles in a pentagon have numerous practical applications in various fields.
- Designing a Pentagon-Shaped Building: The angles in a pentagon are used to create a stable and functional design for a building.
- Creating a Pentagon-Shaped Art Piece: The angles in a pentagon are used to create a visually appealing and thought-provoking art piece.
- Building a Pentagon-Shaped Bridge: The angles in a pentagon are used to create a stable and efficient design for a bridge.
Pentagon Angles Image Gallery
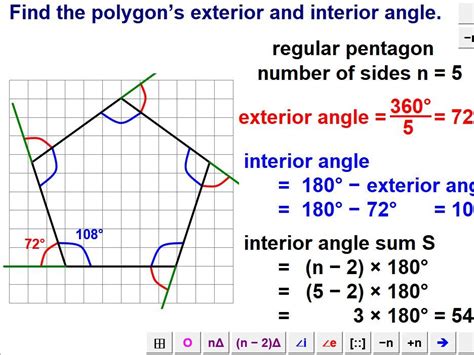


What is the sum of the interior angles of a pentagon?
+The sum of the interior angles of a pentagon is always 540 degrees.
What is the sum of the exterior angles of a pentagon?
+The sum of the exterior angles of a pentagon is always 360 degrees.
What is the interior angle theorem?
+The interior angle theorem states that the sum of the interior angles of a polygon is always (n-2) × 180, where n is the number of sides.
What is the exterior angle theorem?
+The exterior angle theorem states that the sum of the exterior angles of a polygon is always 360 degrees.
What are some practical applications of angles in a pentagon?
+The angles in a pentagon have numerous practical applications in various fields, including architecture, engineering, art, and design.
In conclusion, the angles in a pentagon are a fascinating topic that has numerous applications in various fields. From architecture to engineering, the angles in a pentagon are used to create stable, functional, and visually appealing designs. By understanding the properties and theorems related to angles in a pentagon, we can unlock its full potential and explore new possibilities in various fields.
We hope this article has provided you with a comprehensive understanding of the angles in a pentagon and has inspired you to explore this fascinating topic further. If you have any questions or comments, please feel free to share them with us.
