Mastering George Mason Calculus 3 With Expert Insights

Mastering calculus is a crucial step in developing a deep understanding of mathematics and its applications in various fields. For students at George Mason University, Calculus 3 is a critical course that builds upon the foundations established in Calculus 1 and 2. In this article, we will delve into the world of Calculus 3, providing expert insights and practical tips to help students succeed in this challenging but rewarding course.

Calculus 3 is a course that focuses on the study of multivariable calculus, including vectors, vector functions, and partial derivatives. It also covers topics such as multiple integrals, surface integrals, and differential equations. These concepts are essential in understanding many real-world phenomena, from the motion of objects in space to the behavior of complex systems.

Why is Calculus 3 Important?

Calculus 3 is a critical course for students majoring in mathematics, physics, engineering, and computer science. It provides a deep understanding of mathematical concepts that are used to model and analyze complex systems. By mastering Calculus 3, students can develop problem-solving skills, critical thinking, and analytical reasoning.

Moreover, Calculus 3 is a required course for many graduate programs, including master's and Ph.D. programs in mathematics, physics, and engineering. Students who excel in Calculus 3 are well-prepared to pursue advanced degrees and careers in these fields.

Expert Insights: Tips for Success in Calculus 3

To succeed in Calculus 3, students need to develop a strong foundation in mathematical concepts, including algebra, geometry, and trigonometry. Here are some expert insights and tips to help students master Calculus 3:

Start with a strong foundation: Review algebra, geometry, and trigonometry before starting Calculus 3. Make sure you understand the concepts of functions, graphs, and equations.
Practice consistently: Practice is key to mastering Calculus 3. Set aside time each day to practice problems and review notes.
Use visual aids: Visual aids such as graphs, charts, and diagrams can help students understand complex concepts. Use online resources or graphing calculators to visualize problems.
Work in groups: Collaborate with classmates to work on problems and projects. This can help students stay motivated and learn from each other.

Key Concepts in Calculus 3

Calculus 3 covers a range of topics, including:

Vectors and vector functions: Understand how to work with vectors and vector functions, including operations such as addition, subtraction, and scalar multiplication.
Partial derivatives: Learn how to find partial derivatives and use them to analyze functions of multiple variables.
Multiple integrals: Understand how to evaluate multiple integrals, including double and triple integrals.
Surface integrals: Learn how to evaluate surface integrals and use them to analyze surfaces in three-dimensional space.

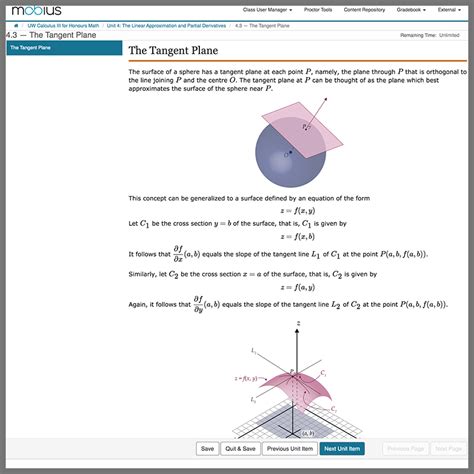
Practical Applications of Calculus 3

Calculus 3 has many practical applications in fields such as physics, engineering, and computer science. Here are some examples:

Physics: Calculus 3 is used to describe the motion of objects in space, including the trajectory of projectiles and the behavior of complex systems.
Engineering: Calculus 3 is used to design and optimize systems, including electronic circuits and mechanical systems.
Computer science: Calculus 3 is used in computer graphics and game development to create realistic models and animations.

Conclusion

Mastering Calculus 3 requires dedication, persistence, and practice. By following these expert insights and tips, students can develop a deep understanding of mathematical concepts and practical applications. Whether you are a student at George Mason University or pursuing a career in mathematics, physics, or engineering, Calculus 3 is an essential course that can help you achieve your goals.

We encourage you to share your thoughts and experiences with Calculus 3 in the comments below. How have you applied Calculus 3 in your studies or career? What tips and resources have helped you master this challenging course?

Calculus 3 Image Gallery

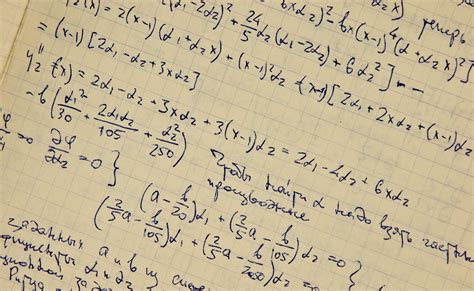
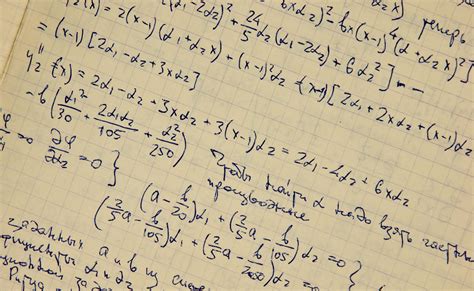
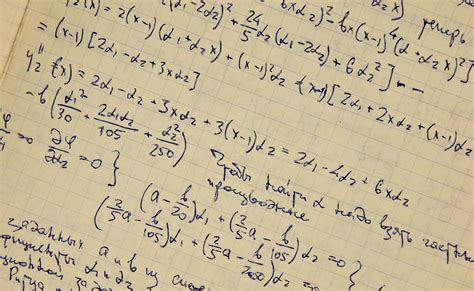
What is Calculus 3?

Calculus 3 is a course that focuses on the study of multivariable calculus, including vectors, vector functions, and partial derivatives.

Why is Calculus 3 important?

What are some practical applications of Calculus 3?

Calculus 3 has many practical applications in fields such as physics, engineering, and computer science. It is used to describe the motion of objects in space, design and optimize systems, and create realistic models and animations.