Find The Prime Factors Of 105 In 3 Easy Steps

The concept of prime factors is a fundamental idea in mathematics, particularly in number theory. Prime factors are the prime numbers that, when multiplied together, give the original number. Finding the prime factors of a number can be a bit challenging, but it can be done in a few easy steps. In this article, we will find the prime factors of 105 in three easy steps.

The process of finding prime factors is essential in various mathematical operations, such as simplifying fractions, finding the greatest common divisor (GCD) of two numbers, and solving algebraic equations. Prime factors are also crucial in cryptography, coding theory, and other areas of mathematics.

Step 1: Understand What Prime Factors Are

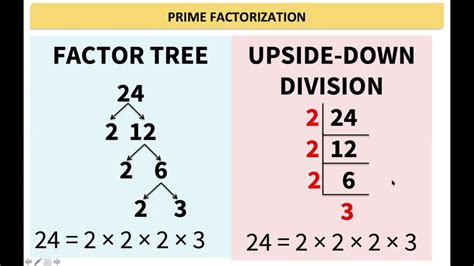
Before we start finding the prime factors of 105, let's first understand what prime factors are. Prime factors are the prime numbers that multiply together to give the original number. For example, the prime factors of 12 are 2, 2, and 3, because 2 × 2 × 3 = 12.

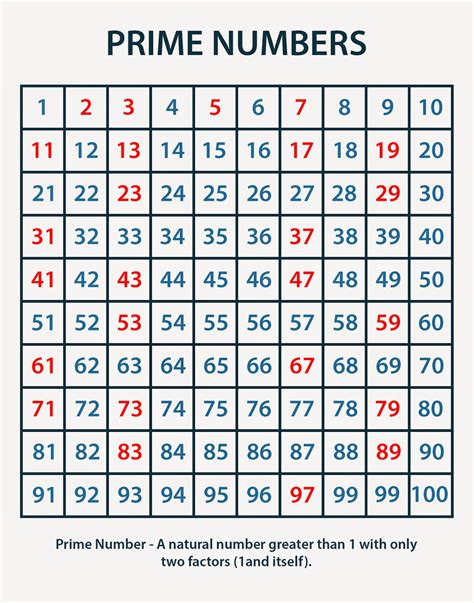
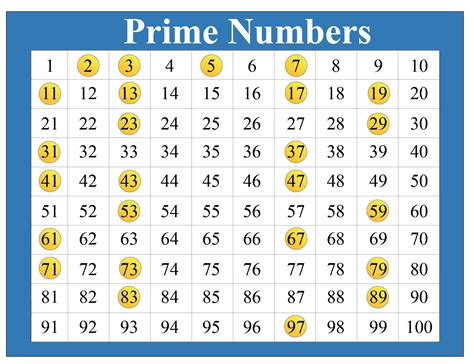
Definition of Prime Numbers

A prime number is a positive integer that is divisible only by itself and 1. In other words, a prime number is a number that is not divisible by any other number except 1 and itself. For example, 2, 3, 5, and 7 are all prime numbers.

Step 2: Find the Prime Factors of 105

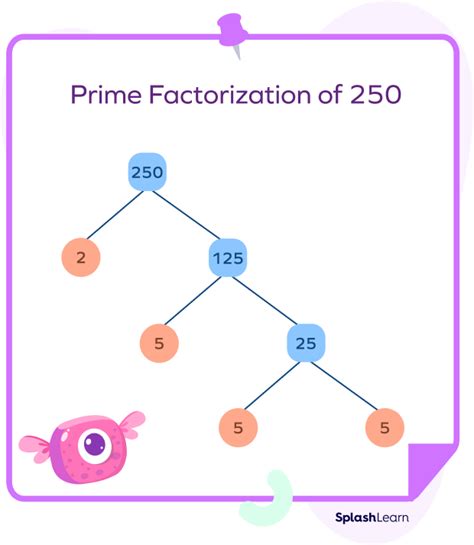
Now that we understand what prime factors are, let's find the prime factors of 105. To do this, we will divide 105 by the smallest prime number, which is 2. However, 105 is not divisible by 2, so we will move on to the next prime number, which is 3.

105 ÷ 3 = 35

Now, we have 35, which is not a prime number. We will divide 35 by the smallest prime number, which is 5.

35 ÷ 5 = 7

Now, we have 7, which is a prime number. Therefore, the prime factors of 105 are 3, 5, and 7.

Why Prime Factors Are Important

Prime factors are essential in various mathematical operations, such as simplifying fractions, finding the greatest common divisor (GCD) of two numbers, and solving algebraic equations. Prime factors are also crucial in cryptography, coding theory, and other areas of mathematics.

Step 3: Verify the Prime Factors

To verify the prime factors of 105, we will multiply the prime factors together to ensure that they give the original number.

3 × 5 × 7 = 105

As we can see, the prime factors of 105 are indeed 3, 5, and 7.

Benefits of Finding Prime Factors

Finding prime factors has several benefits, including:

• Simplifying fractions: By finding the prime factors of the numerator and denominator, we can simplify fractions.
• Finding the GCD: By finding the prime factors of two numbers, we can find the greatest common divisor (GCD) of the two numbers.
• Solving algebraic equations: Prime factors are essential in solving algebraic equations, particularly those involving quadratic equations.

Gallery of Prime Factors

Prime Factors Image Gallery

FAQs

What are prime factors?

+

Prime factors are the prime numbers that multiply together to give the original number.

Why are prime factors important?

+

Prime factors are essential in various mathematical operations, such as simplifying fractions, finding the greatest common divisor (GCD) of two numbers, and solving algebraic equations.

How do I find the prime factors of 105?

+

To find the prime factors of 105, we will divide 105 by the smallest prime number, which is 3. Then, we will divide the result by the next prime number, which is 5, and finally, we will divide the result by the next prime number, which is 7.

We hope this article has helped you understand how to find the prime factors of 105 in three easy steps. Prime factors are an essential concept in mathematics, and finding them can be a bit challenging, but with practice, you will become proficient in no time. If you have any questions or need further clarification, please don't hesitate to ask.