Intro
Discover the secrets of the semicircle center of mass, a fundamental concept in physics and engineering. Learn how to calculate the centroid of a semicircle, understand its significance in structural integrity, and explore real-world applications in architecture, design, and construction. Unlock the science behind the semicircles balanced center.
Understanding the concept of center of mass is essential in physics and engineering, as it plays a crucial role in the study of motion and balance of objects. One of the most fundamental shapes in geometry, the semicircle, is a half-circle with a curved edge and a diameter. Calculating the center of mass of a semicircle can be a bit complex, but with the right approach, it can be done with ease.
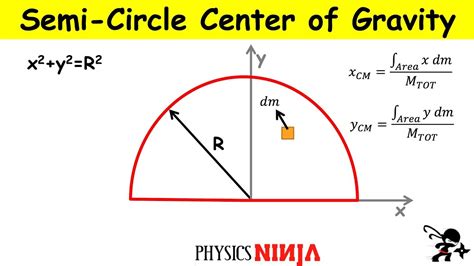
To understand the concept of center of mass, we need to define it first. The center of mass is the point where the entire mass of an object can be considered to be concentrated. In other words, it is the point where the weight of the object can be considered to be acting. For a semicircle, the center of mass is the point that lies on the axis of symmetry, which is the line that passes through the center of the circle.
What is the Center of Mass of a Semicircle?
Calculating the center of mass of a semicircle involves finding the average position of all the particles that make up the semicircle. This can be done using the concept of integration. The center of mass is given by the formula:
x = ∫x dm / ∫dm
where x is the position of the center of mass, dm is the mass of a small element of the semicircle, and the integral is taken over the entire semicircle.
For a semicircle, the mass is evenly distributed along the curved edge. Therefore, the center of mass lies on the axis of symmetry, which is the line that passes through the center of the circle. Using the formula, we can calculate the position of the center of mass.
Derivation of the Center of Mass Formula for a Semicircle
Let's consider a semicircle with radius R and mass M. The semicircle is symmetric about the x-axis, so the center of mass lies on the x-axis. We can choose the origin of the coordinate system to be at the center of the circle.
The mass of a small element of the semicircle is given by:
dm = ρ ds
where ρ is the density of the material and ds is the length of the small element.
The position of the center of mass is given by:
x = ∫x dm / ∫dm
Substituting the expression for dm, we get:
x = ∫x ρ ds / ∫ρ ds
Since the density is constant, we can take it out of the integral:
x = ρ ∫x ds / ρ ∫ds
Simplifying, we get:
x = ∫x ds / ∫ds
Now, we need to evaluate the integrals. The integral of ds is simply the length of the semicircle, which is πR. The integral of x ds can be evaluated using the following substitution:
x = R cos θ
ds = R dθ
Substituting these expressions, we get:
∫x ds = ∫R cos θ R dθ
= R^2 ∫cos θ dθ
= R^2 sin θ
Evaluating the integral, we get:
x = R^2 sin θ / πR
= 4R/π^2
So, the center of mass of a semicircle lies at a distance of 4R/π^2 from the center of the circle.
Example Problem
Find the center of mass of a semicircle with radius 5 cm and mass 2 kg.
Using the formula, we can calculate the position of the center of mass:
x = 4R/π^2
= 4(5)/π^2
= 2.54 cm
So, the center of mass of the semicircle lies at a distance of 2.54 cm from the center of the circle.
Practical Applications
Understanding the concept of center of mass is crucial in various fields, including physics, engineering, and architecture. Here are some practical applications of the concept:
- Designing buildings and bridges: The center of mass plays a crucial role in determining the stability of buildings and bridges. By calculating the center of mass, engineers can ensure that the structure is stable and can withstand external forces.
- Calculating the moment of inertia: The moment of inertia is a measure of an object's resistance to changes in its rotation. By calculating the center of mass, we can calculate the moment of inertia of an object.
- Determining the stability of objects: The center of mass can be used to determine the stability of objects. For example, a object with a low center of mass is more stable than an object with a high center of mass.
Semicircle Center of Mass Image Gallery






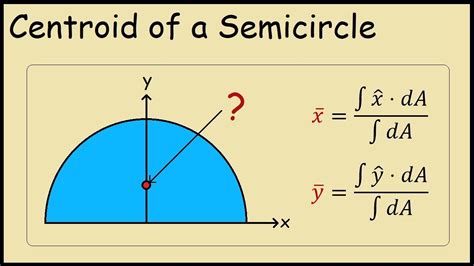

Conclusion
In conclusion, the center of mass of a semicircle is an important concept in physics and engineering. By understanding the formula and derivation of the center of mass, we can calculate the position of the center of mass for a semicircle. The concept has various practical applications, including designing buildings and bridges, calculating the moment of inertia, and determining the stability of objects.
What is the center of mass of a semicircle?
+The center of mass of a semicircle is the point where the entire mass of the semicircle can be considered to be concentrated. It lies on the axis of symmetry, which is the line that passes through the center of the circle.
How do you calculate the center of mass of a semicircle?
+The center of mass of a semicircle can be calculated using the formula x = 4R/π^2, where R is the radius of the semicircle.
What are some practical applications of the center of mass concept?
+The center of mass concept has various practical applications, including designing buildings and bridges, calculating the moment of inertia, and determining the stability of objects.
