Speed Of Sound In Knots Explained Simply

The speed of sound is a fundamental concept in physics that plays a crucial role in various fields, including aviation, acoustics, and weather forecasting. While it's commonly expressed in units of meters per second or miles per hour, it's also essential to understand its equivalent in knots, particularly for sailors and pilots. In this article, we'll delve into the speed of sound in knots, its significance, and how it's calculated.

Understanding the Speed of Sound

The speed of sound is the velocity at which sound waves propagate through a medium, such as air, water, or solids. It's an intrinsic property of the medium itself and depends on its temperature, pressure, and density. In dry air at room temperature and atmospheric pressure, the speed of sound is approximately 343 meters per second (m/s) or 768 miles per hour (mph).

Converting Speed of Sound to Knots

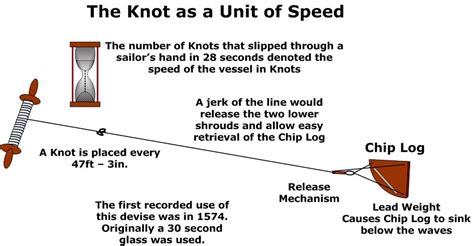
A knot is a unit of speed equivalent to one nautical mile per hour. To convert the speed of sound from meters per second or miles per hour to knots, we need to use the following conversion factors:

1 knot = 1.852 kilometers per hour (km/h) = 1.15078 miles per hour (mph)

Using these conversion factors, we can calculate the speed of sound in knots as follows:

Speed of sound (m/s) x (1 km/h / 1000 m/s) x (1 knot / 1.852 km/h) ≈ 661.48 knots

Alternatively, we can use the speed of sound in miles per hour and convert it directly to knots:

Speed of sound (mph) x (1 knot / 1.15078 mph) ≈ 661.48 knots

Why is the Speed of Sound Important in Knots?

Understanding the speed of sound in knots is essential for various applications, particularly in aviation and navigation. Here are a few reasons why:

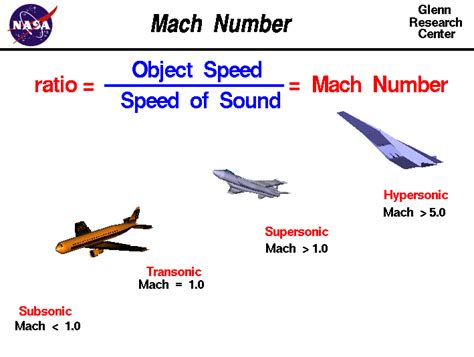
• Aviation: When an aircraft breaks the sound barrier, it produces a sonic boom, which can be harmful to people on the ground. By understanding the speed of sound in knots, pilots can estimate the aircraft's speed relative to the sound barrier and take necessary precautions.
• Navigation: In maritime navigation, the speed of sound in knots helps calculate distances and velocities. For example, when using radar or sonar to detect objects, the speed of sound is used to calculate the time it takes for sound waves to travel between the transmitter and receiver.
• Weather Forecasting: The speed of sound is also crucial in weather forecasting, particularly when predicting storm patterns and wind speeds. By understanding how sound waves propagate through different mediums, meteorologists can better predict weather patterns and issue timely warnings.

Calculating the Speed of Sound in Different Mediums

The speed of sound varies significantly depending on the medium it travels through. Here are some examples of how to calculate the speed of sound in different mediums:

• Air: The speed of sound in air can be calculated using the following formula: Speed of sound (m/s) = 331.5 + (0.6 x temperature in °C)
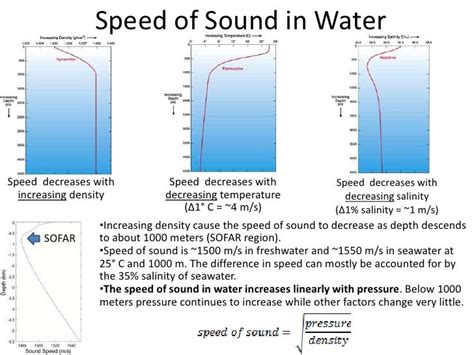
• Water: The speed of sound in water is approximately 1,482 m/s at room temperature and atmospheric pressure.
• Solids: The speed of sound in solids depends on the material's properties, such as its density and elastic modulus. For example, the speed of sound in steel is approximately 5,960 m/s.

Practical Applications of the Speed of Sound in Knots

The speed of sound in knots has several practical applications in various fields, including:

• Sonic Booms: As mentioned earlier, when an aircraft breaks the sound barrier, it produces a sonic boom. By understanding the speed of sound in knots, pilots can estimate the aircraft's speed relative to the sound barrier and take necessary precautions.
• Radar and Sonar: The speed of sound is used in radar and sonar systems to calculate distances and velocities. For example, when using radar to detect objects, the speed of sound is used to calculate the time it takes for sound waves to travel between the transmitter and receiver.
• Weather Forecasting: The speed of sound is also crucial in weather forecasting, particularly when predicting storm patterns and wind speeds. By understanding how sound waves propagate through different mediums, meteorologists can better predict weather patterns and issue timely warnings.

Conclusion

In conclusion, the speed of sound in knots is an essential concept that plays a significant role in various fields, including aviation, navigation, and weather forecasting. By understanding the speed of sound in knots, we can better appreciate its practical applications and importance in our daily lives. Whether you're a pilot, sailor, or meteorologist, knowing the speed of sound in knots can help you make more informed decisions and take necessary precautions.

Gallery of Speed of Sound

Speed of Sound Image Gallery

FAQs

What is the speed of sound in knots?

+

The speed of sound in knots is approximately 661.48 knots.

Why is the speed of sound important in knots?

+

The speed of sound in knots is essential for various applications, including aviation, navigation, and weather forecasting.

How is the speed of sound calculated in different mediums?

+

The speed of sound in different mediums can be calculated using various formulas, such as the speed of sound in air (331.5 + 0.6 x temperature in °C) or the speed of sound in water (approximately 1,482 m/s at room temperature and atmospheric pressure).

We hope this article has helped you understand the speed of sound in knots and its significance in various fields. If you have any questions or comments, please feel free to share them below.