Intro
Unlock the secrets of the Pentagon Area Equation and Formula. Discover how to calculate the area of a pentagon using simple math formulas and equations. Learn the step-by-step process, explore geometric properties, and understand the significance of pentagons in real-world applications. Dive into the world of geometry and boost your math skills.
Pentagons are five-sided polygons that have been a fascination for mathematicians and architects alike for centuries. Whether you're trying to calculate the area of a pentagonal building or a geometric shape, understanding the pentagon area equation and formula is crucial.
The importance of calculating the area of a pentagon lies in its numerous real-world applications, from designing buildings and bridges to solving complex mathematical problems. In this article, we'll delve into the world of pentagons, exploring their properties, types, and most importantly, how to calculate their area using the pentagon area equation and formula.
What is a Pentagon?
A pentagon is a five-sided polygon with five vertices and five sides. The sum of the interior angles of a pentagon is always 540 degrees, and the sum of the exterior angles is always 360 degrees. Pentagons can be regular or irregular, depending on the length of their sides and the measure of their angles.
Types of Pentagons
There are several types of pentagons, including:
- Regular pentagon: A pentagon with all sides and angles equal.
- Irregular pentagon: A pentagon with unequal sides and angles.
- Convex pentagon: A pentagon with all interior angles less than 180 degrees.
- Concave pentagon: A pentagon with at least one interior angle greater than 180 degrees.
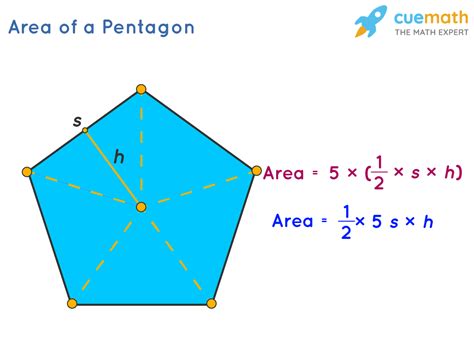
Pentagon Area Equation and Formula
The area of a pentagon can be calculated using the formula:
Area = (n * s^2) / (4 * tan(π/n))
Where:
- n is the number of sides (5 for a pentagon)
- s is the length of one side
- π is a mathematical constant representing the ratio of a circle's circumference to its diameter (approximately 3.14159)
- tan is the tangent function
For a regular pentagon, the formula can be simplified to:
Area = (5 * s^2) / (4 * tan(π/5))
Where s is the length of one side.
How to Calculate the Area of a Pentagon
To calculate the area of a pentagon, follow these steps:
- Determine the length of one side (s) of the pentagon.
- Plug the value of s into the formula: Area = (5 * s^2) / (4 * tan(π/5))
- Calculate the value of tan(π/5) using a calculator or mathematical software.
- Multiply 5 by the square of s (s^2).
- Divide the result by 4 times the value of tan(π/5).
- The resulting value is the area of the pentagon.
Example: Calculating the Area of a Regular Pentagon
Suppose we have a regular pentagon with each side measuring 6 inches. To calculate the area, we plug the value of s into the formula:
Area = (5 * 6^2) / (4 * tan(π/5))
First, we calculate the value of tan(π/5) using a calculator:
tan(π/5) ≈ 0.7265
Next, we multiply 5 by the square of s (s^2):
5 * 6^2 = 180
Then, we divide the result by 4 times the value of tan(π/5):
180 / (4 * 0.7265) ≈ 61.937
Therefore, the area of the regular pentagon is approximately 61.937 square inches.
Practical Applications of the Pentagon Area Equation and Formula
The pentagon area equation and formula have numerous practical applications in various fields, including:
- Architecture: Calculating the area of pentagonal buildings, bridges, and other structures.
- Engineering: Designing pentagonal shapes for mechanical and electrical components.
- Mathematics: Solving complex mathematical problems involving pentagons and other polygons.
Gallery of Pentagon-Related Images
Pentagon Image Gallery





FAQs
What is the formula for the area of a pentagon?
+The formula for the area of a pentagon is (n \* s^2) / (4 \* tan(π/n)), where n is the number of sides and s is the length of one side.
How do I calculate the area of a regular pentagon?
+To calculate the area of a regular pentagon, plug the value of s into the formula: Area = (5 \* s^2) / (4 \* tan(π/5)), and solve for the area.
What are some practical applications of the pentagon area equation and formula?
+The pentagon area equation and formula have numerous practical applications in architecture, engineering, mathematics, and design.
Conclusion
In conclusion, understanding the pentagon area equation and formula is essential for solving complex mathematical problems and real-world applications. By following the steps outlined in this article, you can calculate the area of a pentagon with ease. Whether you're an architect, engineer, or mathematician, the pentagon area equation and formula are valuable tools to have in your toolkit.
